“最近写论文用到了EKF,以前都只是对滤波问题了解工程上的大概,这次对相关知识做一个系统性的总结。
参考资料:
一、卡尔曼滤波感性认识
一个卡尔曼滤波的典型应用是用于传感器融合。以Matlab视频中的简单例子作一个初步的感性认识。
假设一个小车在行驶的过程中,我们想要知道小车的具体位置,我们有两种方式可以获取它的位置信息:
- 已知小车$t-1$时刻的位置、速度、加速度等信息,我们可以通过运动学公式计算出小车理想状态在t时刻的位置 $\hat{P1}$;
- 同样,如果我们在$t$时刻采用GPS定位,也能得到小车的位置信息 $\hat{P2}$。
然而,在第一种方法中,小车由于天气因素,车轮滑动等各种原因引起的误差,使得该计算值 $\hat{P1}$ 并不精确;而GPS由于精度的原因,其输出的小车具体位置 $\hat{P2}$ 同样存在误差。那么如何结合这两个估计值 $\hat{P1}$ 和 $\hat{P2}$,获得比较精确的小车的实际位置呢?
直觉上能想到的可以直接将两个值做平均,做为小车实际位置的估计。当然,也可以找出一个你比较信任的值,给与比较大的权重,做加权平均,如 0.7 * $\hat{P1}$ + 0.3 * $\hat{P2}$。事实上,卡尔曼滤波的核心思想和这种思路非常相似。
实际上,由于误差的存在,$\hat{P1}$ 和 $\hat{P2}$ 可以看做是两个随机分布。通过$t-1$时刻估算出的$t$时刻小车位置的概率分布如下图所示:

而通过GPS测量,小车位置的概率分布如下图所示:
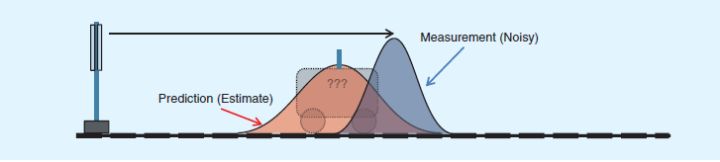
假设两个随机分布服从高斯分布,那么通过卡尔曼滤波算法(找到一个加权的值)计算出的最终小车位置的分布结果为下图中绿色的部分:

最终得出小车位置的实际估算位置(分布/区间)。
二、卡尔曼滤波算法详述
上面的文字描述只是为了形象地描述卡尔曼滤波的功能有一个感性的认识。下面这一节对算法和背后的一些理论做一些详细记录。
2.1 卡尔曼滤波系统模型
卡尔曼滤波有两个重要的方程(系统离散状态方程),即:
从$k-1$到$k$时刻的系统状态预测方程,表示如何通过$k-1$的状态得出$k$状态(即上文中的通过运动学公式的计算的小车位置):
\[X_k = AX_{k-1} + Bu_k +w_k\]系统状态观测方程(观测得出的,即上文中所说的GPS观测的小车位置):
\[Z_k = HX_k +v_k\]其中$X_k$,$X_{k-1}$为系统在$k$时刻和$k-1$时刻的状态,$A$为状态转移矩阵,$B$为系统输入增益矩阵,$u_k$为系统输入,$w_k$和$v_k$分别为计算的噪声和观测的噪声(均服从正态分布),$H$为测量矩阵。
如果不太清楚方程1在实际例子中是如何对应的,此处再结合前文中关于小车的例子进一步进行直观解释,假设我们想要知道的小车状态为距离$d$和速度$v$(即$X$变成了一个向量包含两个值)。假设我们已知$k-1$时刻的$d_{k-1}$和$v_{k-1}$,又知道加速度$a$,时间间隔为$t$,那么根据运动学公式(高中知识):
\[d_k = d_{k-1} + v_{k-1} + 1/2at^2\]
\[v_k = v_{k-1} + at\]
那么在公式$ X_k = AX_{k-1} + Bu_k +w_k $中的各项分别为:
\[X_t = [d, v] ^\mathrm{T}\]
\[A = \left[ \begin{matrix} 1 & t \\ 0 & 1 \\ \end{matrix} \right]\]
\[u_t = a\]
\[B = [1/2t^2 ,t] ^\mathrm{T}\]
2.2 卡尔曼滤波算法过程
卡尔曼估计实际由两个过程组成:预测与更新,在预测阶段,滤波器使用上一状态的估计,做出对当前状态的预测。在更新阶段,滤波器利用对当前状态的观测值修正在预测阶段获得的预测值,以获得一个更接进真实值的新估计值。
预测过程:
\[\hat{x_k}'= A \hat{x_{k-1}} + Bu_k\] \[P_k' = AP_{k-1}A^\mathrm{T} + Q\]其中各个变量的含义分别为:
$\hat{x_k}$ :卡尔曼估计值; $\hat{x_k}’$:预测值; $P_{k}$:卡尔曼估计协方差矩阵; $P_{k}’$:预测协方差矩阵;
可以看出,预测过程是要预测值以及预测协方差矩阵(即多少误差)。此处对应一维卡尔曼滤波预测过程的均值计算和方差计算。式2中分别为uk带来的协方差和估算本身的协方差。
更新过程:
\[\hat{z_k} = z_k -H\hat{x_k}'\] \[K_k = P_k'H^T(HP_k'H^T+R)^{-1}\] \[\hat{x_k} = \hat{x_k}' + K_k\hat{z_k}\]此处$K_k$:卡尔曼增益;$z_k$:测量余量。
更新过程即为将小车的计算值和GPS值的两个高斯分布相乘的过程,根据协方差得出的$K_k$可以看做是某种意义的权重。
最后更新协方差估计:
\[P_k = (I - K_kH)P_k'\]可以认为,算法的大致流程就是首先对值和误差做预测,随后通过观测值对这个预测值做一个校正,校正的权重即为卡尔曼增益。并将校正后的值当做真实值,并作为下一次迭代的输入。这里算法核心是卡尔曼增益$K_k$,和协方差相关($P_{k}’$)的推导过程,此处不再做细节推导,可以参考此处和此处,这两篇文章比较清晰。大致上说,$K_k$的推导思路是最大似然的思路,就是求出使得均方误差最小的那个值。而$K_k$的物理意义就是在观测值和计算值之间的一个权值,如果很大则偏向观测值,如果很小则偏向预测值。
2.3 卡尔曼滤波算法应用场景和条件
通过上述的推导大致了解了卡尔曼滤波的整个过程,个人再简单理解下,就是带误差的预测值(通过k-1状态预测k)和带误差的观测值(在k时刻直接观测)分别都是高斯分布,因为假设误差本身就是服从高斯分布。那么如果想要同时满足两个分布,则将两个分布相乘即可。
而卡尔曼滤波的局限在于,系统的传递函数(即递推公式 $ \hat{x_k}’= A \hat{x_{k-1}} + Bu_k $)必须是线性的。因为如果是一个非线性的函数,递推之后的$x_k$就不服从高斯分布,假设就不成立了。为了满足这一点,后续就引出了EKF等一系列的滤波器,关于EKF及其之后的介绍将在下一篇文章讲述。
文章最后,贴上一段来自灵剑大佬从信号与系统的角度对卡尔曼滤波的理解,感觉很有启发:
“ 信号处理中的滤波实质上就是讲降噪。一个信号通常是有用的原始信号与一个噪声的叠加,噪声一般用高斯白噪声描述,它们混在一起了,我放大信号噪声也放大,缩小噪声信号也缩小,一般我没有通用办法改善信噪比。但是如果我有好几个信号,里面包含了相同的原始信号,我把它们叠加在一起,原始信号是相干叠加,幅度变成两倍功率变成了四倍,而噪声是非相干叠加,许多地方会相互抵消,功率只变成两倍,这样信噪比就提高了一倍。所有的“滤波”降噪,本质上都是通过相干叠加增强原始信号提高信噪比的。上面的情况是信噪比相同,如果信噪比不同呢?用一步柯西不等式就能证明,对于噪声功率相同的信号,只要按各自信号功率比例混合,就能最大化信噪比。最后,如果不是另采了一个信号,而是用历史测量值来预测,将预测值作为另一个信号,这个预测值的信噪比是可以推算出来的,再采用前面的方法就得到卡尔曼滤波。